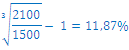RAČUNOVODSTVO PAVLIHA

ČASOVNA VREDNOST DENARJA

PRIMER 1

Glavnica = 1,000€
Letna obrestna mera = 10%
Število obdobij = 2

NA VRH

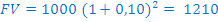
PRIMER 2

Koliko bo vredna začetna naložba 100€ čez sedem let pri letni obrestni meri 9%.

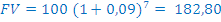
Torej 182,80€

NA VRH

PRIMER 3

V začetku prvega leta vložimo na banko 1000€, v začetku drugega 500€ in v začetku tretjega leta 600€. Kolikšna je prihodnja vrednost na koncu tretjega leta, če je letna obrestna mera 9%.

Enačba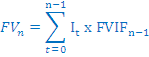

v tem primeru zgleda takole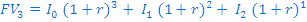

Vplačila	FVIF	I0 x FVIF
1.000,00€	1,093 = 1,295029	1.1295,03€
500,00€	1,092 = 1,1881	594,05€
600,00€	1,091 = 1,09	654,00€
2.100,00€		2.543,08€

Prihodna vrednost vloge konec tretjega leta znaša 2.543,08€

NA VRH

PRIMER 4

Koliko moramo vložiiti v banko danes, da bomo čez 4 leta lahko kupili avto za 20.000€, če je letna obrestna mera 6%

NA VRH

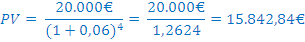
PRIMER 5

Državna obveznica nam obljublja naslednja izplačila vsak konec leta in sicer konec prvega leta 1.000€, konec drugega 1.100€, konec tretjega leta pa 1.200€. Diskontna stopnja je 8%. Izračuna neto sedanjo vrednost.

Enačba

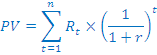
za za posebni primer zgleda takole

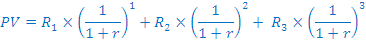
Donosi	DF	R x DF
1.000,00€	0,9259	925,90€
1.100,00€	0,8573	943,03€
1.200,00€	0,7938	952,56€
3.300,00€		2.821,49€

Donosi državnih obveznic so na današnji dan vredni 2.821.49€

NA VRH

PRIMER 6

Na razpolago imamo 100 000€, ki jih lahko investiramo za 3 leta. Obrestne mere na hranilne vloge znašajo 5%, medtem ko državne obveznice prinašajo 8% letne obresti. Koliko bo vrednih naših 100 000€ čez tri leta, če jih vložimo na hranilno knjižico ali če kupimo državne obveznice

NA VRH

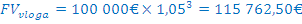
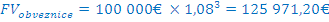
PRIMER 7

Študent Peter želi na smučanje, to pa ga bo stalo 3.000€. Leta 1990 znašajo njegovi prihranki 2.253,94€. Po najmanj kakšni obresti meri mora Peter naložiti svoje prihranke leta 1990, da bo imel čez tri leta dovolj denarja za smučanje

Izpeljemo obrazec 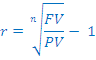in vstavimo podatke

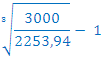
Peter bi moral naložiti svoje prihranke vsaj po 10% letni obrestni meri.

NA VRH

PRIMER 8

Kolikšna je stopnja donosa investicije, pri kateri morate danes plačati polog 40.000€ in dobite čez 10 let izplačanih 100.000€?

Izpeljemo enačbo 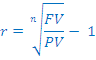in vstavimo podatke

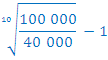
Stopnja donosa je 9,59%

NA VRH

PRIMER 9

Poslovni partner nam ponuja naložbo, ki obljublja izplačilo 60.000€ ob koncu šestega leta in 60.000€ ob koncu dvanajstega leta. Zahtevana donosnost je 10%. Koliko moramo vložiti danes, da bomo dobili ta izplačila?

Enačba za sedanjo vrednost večkratnih plačil je

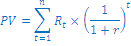
Vstavimo naše podatke in dobimo

NA VRH

PRIMER 10

Pred kratkim smo zadeli na loteriji. Zadetek je izplačljv na dva načina:

Diskontna stopnja je 8%

Iz izračuna v excelovi tabeli je vidno da je današnja vrednost prihodnjih donosov 971.297,24€. Glede na to, da je takojšnje izplačilo 1.125.000€ se bomo odločili za takojšnje izplačilo

NA VRH

PRIMER 11

Zavarovalniški zastopnik bi vas rad navdušil za naslednjo obliko zavarovanja. V primeru da prihodnjih 10 let vsako leto plačate zavarovalnici 150.000€ boste od 25.leta dalje dobivali 15 let vsako leto 250.000€. Diskontna stopnja je 6%. Ali bi se odločili za to zavarovanje?

Izračun

Iz primerjave neto sedanje vrednosti vplačil in izplačil sledi, da je neto sedanja vrednost vplačil 1.104.013,06€, neto sedanja vrednost izplačil pa 599.679,29€. Torej se za to naložno ne bomo odločili.

NA VRH

PRIMER 12

Kolikšna je stopnja donosnosti investicije, pri kateri morate danes plačati polog € 400.000 in dobite čez 10 let izplačanih € 1 mio?

Poslovni partner pa vam ponuja naložbo, ki obljublja izplačilo € 600.000 ob koncu šestega leta ter € 600.000 ob koncu dvanajstega leta. Glede na tveganje je zahtevana stopnja donosa 10 %

Kateri investiciji bi dali prednost, če bi se morali odločiti le za eno izmed obeh možnosti?

Iz enačbe 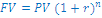izračunamo

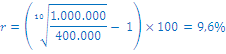
Stopnja donosnosti investicije je 9,6%

Za izračun neto sedanje vrednosti prihodnjih donosov uporabimo enačbo 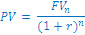in sicer je neto sedanja vrednost dveh plačil po 600.000€ na koncu šestega in dvanajstega leta

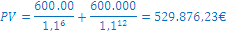
Odločil bi se za drugo možnost, ker je neto sedanja vrednost 529.876,23€ in to je več kot 400.000€

NA VRH

PRIMER 13

Franc Koren ima na razpolago € 100.000, ki jih je pripravljen investirati za obdobje treh let. Obrestne mere na hranilne vloge trenutno znašajo 6 %, medtem ko državne obveznice prinašajo 8 %-ne letne obresti. Izračunajte, koliko bo vrednih Francetovih € 100.000 čez tri leta, če jih vloži na hranilno knjižico ali če kupi državno obveznico!

Uporabimo enačbo 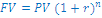in izračunamo

NA VRH

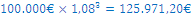
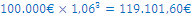
PRIMER 14

V začetku leta t-1 ste na hranilno knjižico vložili € 60.000. Čez eno leto ste vložili dodatnih € 80.000 in čez dve leti še € 100.000. Konec leta t+3 želite dvigniti s hranilne knjižice vse prihranke, ki so se obrestovali po 8 %-ni letni obrestni meri. Koliko denarja boste dvignili?

t-1	t	t+1	t+2	t+3
60.000	80.000		100.000	dvig

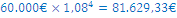
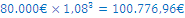
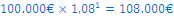
Skupaj bo dvig znašal 290.406,29€

NA VRH

PRIMER 15

Študent VŠP Sebastian se zelo rad smuča in želi zimo leta t+3 preživeti v Vailu v ZDA. Meni, da bi ga to stalo približno € 2.100. Danes, leta t, znašajo njegovi prihranki natanko € 1.500. Po najmanj kakšni obrestni meri mora Sebastian naložiti svoje prihranke danes, leta t, da bo imel čez tri leta dovolj denarja za smučanje v ZDA?

Iz enačbe 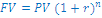preračunamo enačbo 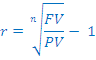in dobimo rezultat

NA VRH

formulex formule